Equações do 2 grau
1) Resolva em R a equação 3 x² – x – 2 = 0
2) Encontre as raízes reais que formam o conjunto solução da equação do segundo grau: 2x² – 7x = 0
3) Ache as raízes reais, se houverem, para a equação incompleta:
4x² + 2 = 0
4) A equação incompleta 4x² – 16 = 0 possui solução? Se sim, quais são as raízes reais que a resolvem?
5) Por que a equação 5x² + 8x + 10 = 0 não possui raízes reais?
Gabarito
1) Coeficientes: a = 3; b = - 1; c = - 2
Primeiro passo, encontrar o delta: (Δ = b² – 4 . a . c)
Δ = b² – 4 . a . c
Δ = (-1)² – 4 . 3 . (-2)
Δ = 1 + 24
Δ = 25
Segundo passo, aplicar a fórmula de Bháskara:

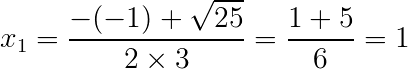
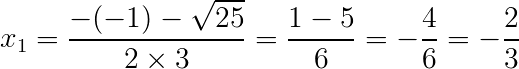
Portanto, o conjunto solução da equação é: S = {1, -2/3}
2) É fácil perceber que uma das raízes que satisfaz a equação é 0 (zero).
Portanto, temos uma equação do segundo grau incompleta com c = 0.
Dessa forma, encontraremos a outra raiz.
Coeficientes:a = 2; b = - 7;c = 0
Resolvendo:
2x² – 7x = 0
x . ( 2x - 7) = 0
x= 0 e 2x - 7 = 0
2x = 7
x = 7/2
Então o conjunto solução da equação é: S = {0; 7⁄2}
3) Temos uma equação do segundo grau incompleta com
b = 0.
Portanto, uma das soluções da equação não será zero:
Coeficientes:
a = 4
b = 0
c = 2
Resolvendo, temos:
4x² + 2 = 0
4x² = - 2
x² = - 2 /4
x = √-2/4 (∄ raízes reais)
Como não existe raízes reais para números negativos, o conjunto solução é: S ={Ø}
4) Sim. Temos uma equação do 2º grau incompleta com
b = 0. Dessa forma, podemos respondê-la aplicando a fórmula do exercício anterior.
Sendo assim, temos:
Coeficientes: a = 4; b = 0; c = -16
4x² – 16 = 0
x² =16/4
x² = 4
x =√4
x =± 2
Portanto, o conjunto solução da equação é: S = {-2, +2}
5) Temos uma equação completa, com coeficientes: a = 5; b = 8; c = 10
Primeiro passo para achar as raízes que satisfazem uma equação completa do 2º grau é encontrar o valor do discriminante delta:
Δ = b² – 4 . a . c
Δ = 8² – 4 . 5 . 10
Δ = 64 – 200
Δ = – 136
Portanto, como Δ < 0, ou seja, delta é negativo, a equação não admite solução em R.
Nenhum comentário:
Postar um comentário